The Role of Mean Absolute Deviation Function in Obtaining Smooth Estimation for Distribution and Density Functions: Beta Regression Approach

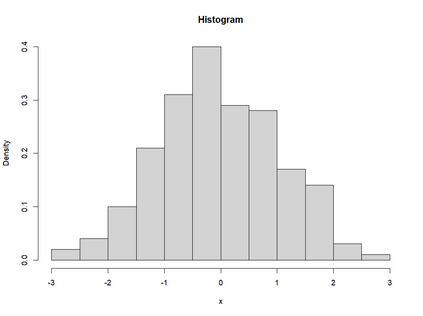
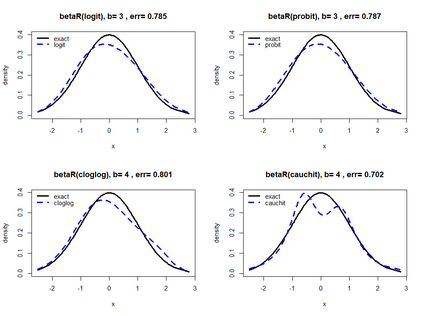
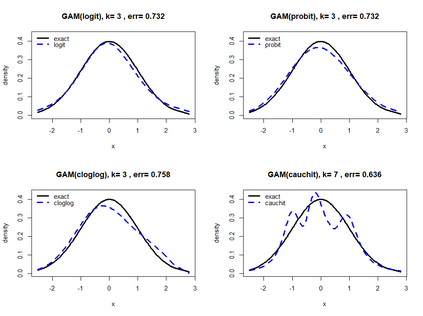
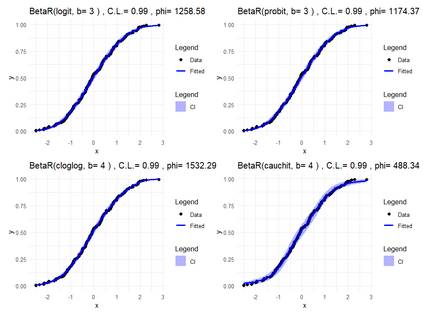
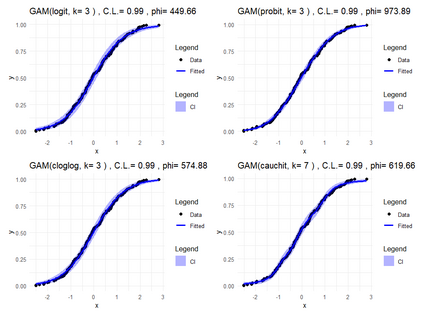
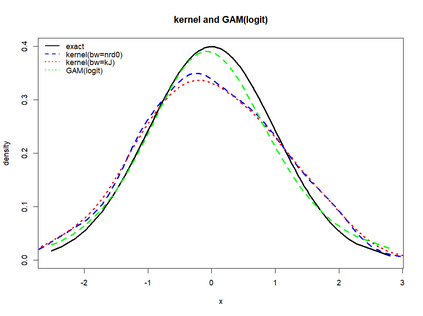
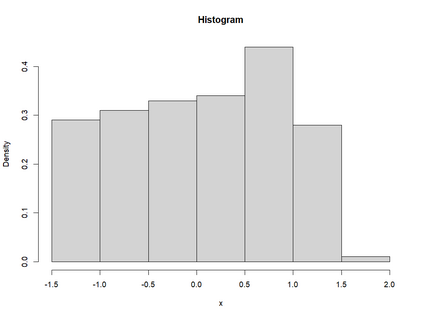
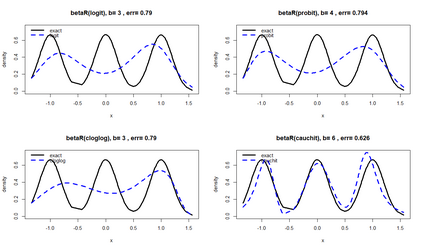
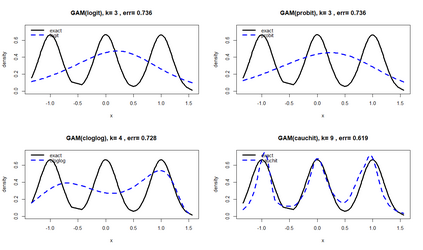
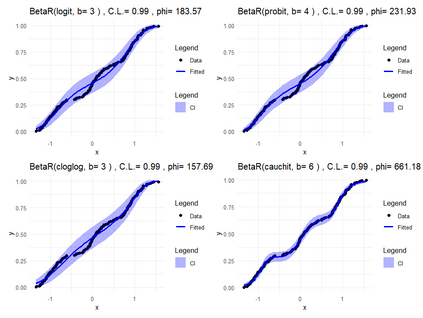
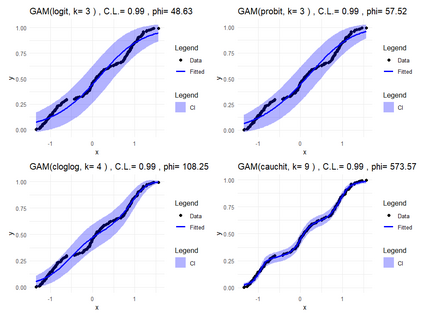
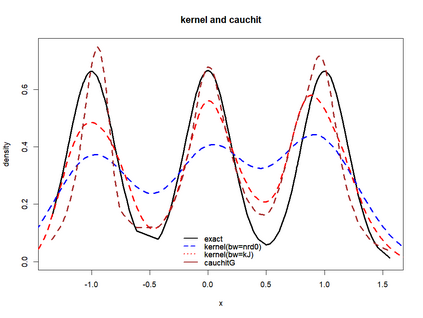
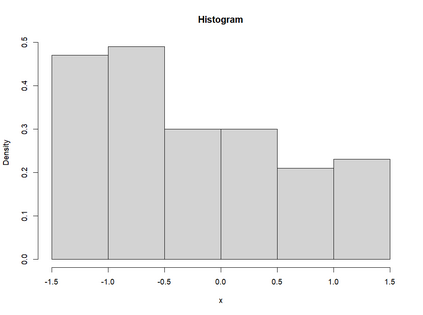
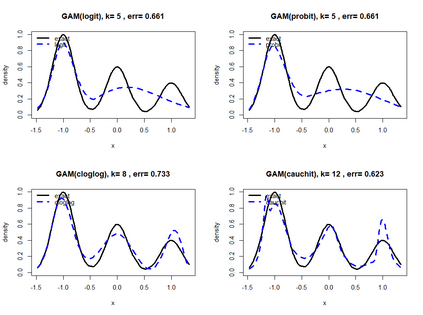
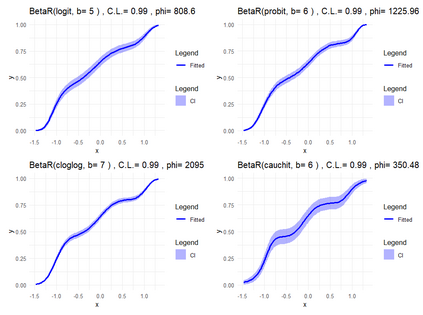
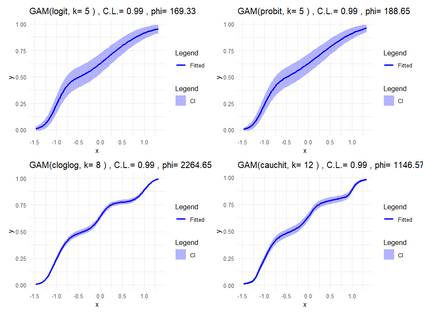
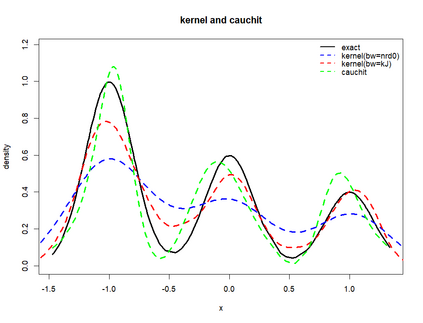
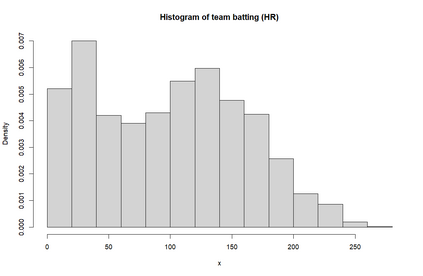
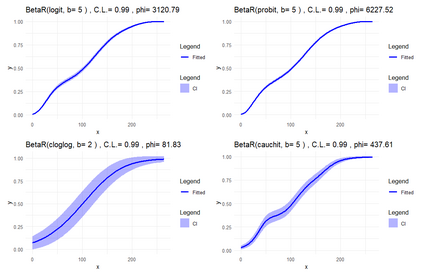
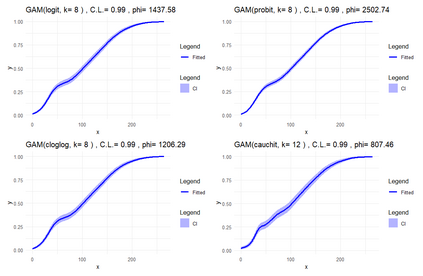
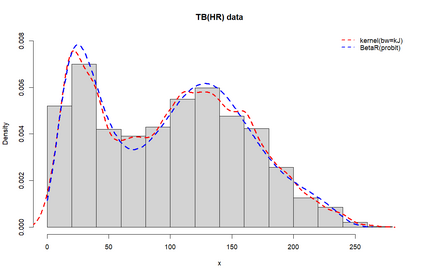
Smooth Estimation of probability density and distribution functions from its sample is an attractive and an important problem that has applications in several fields such as, business, medicine, and environment. This article introduces a simple approach but novel for estimating both functions via beta regression and generalized additive model approaches. The approach explores estimation of both functions by smoothing the first derivative of left mean absolute deviation function to obtain the final optimal smooth estimates under the condition of nondecreasing distribution function, and the density function remains nonnegative. This is achieved by using beta regression and generalized additive model with various link functions (logit, probit, cloglog, and cauchit) that applied to a polynomial function whose degree is determined by less mean absolute regression errors. Additionally, confidence limits for the distribution function are derived based on the beta distribution to give judgement about precision of obtained estimates. The method is utilized on simulated datasets featuring unimodal and multimodal and an actual dataset. The results suggest that this method exhibits strong performance relative to the kernel-based method, especially for its superior attributes in sample sizes and smoothness.