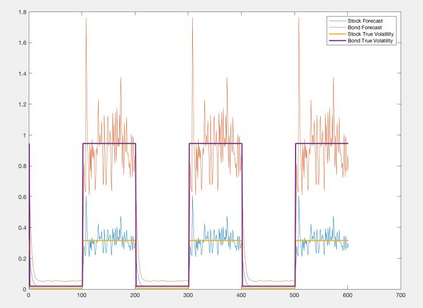
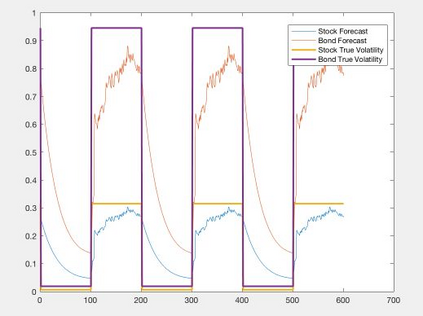
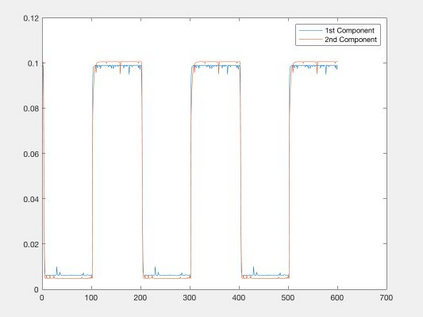
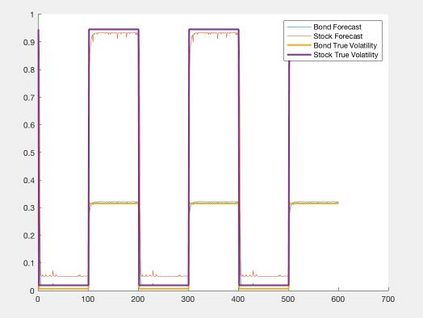
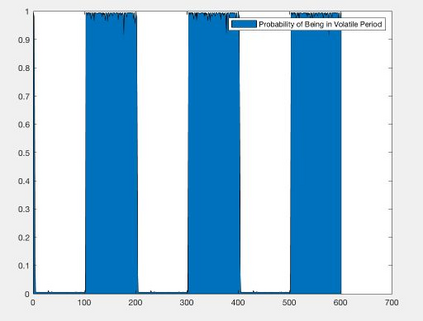
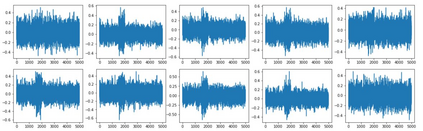
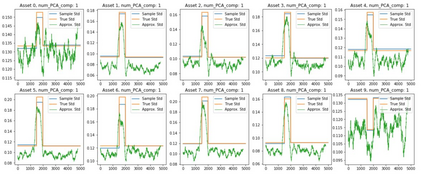
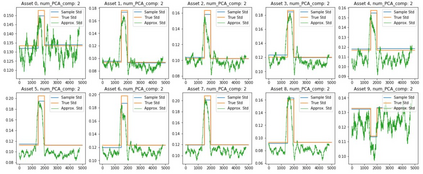
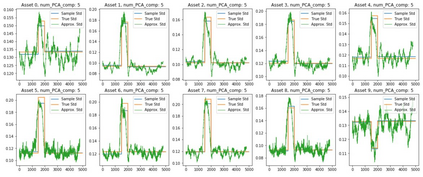
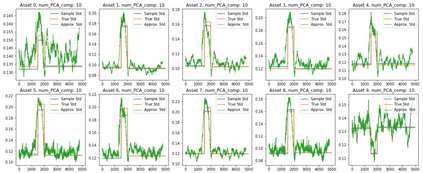
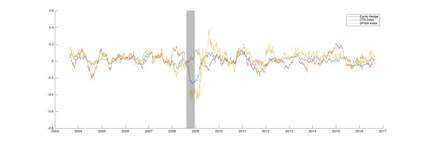
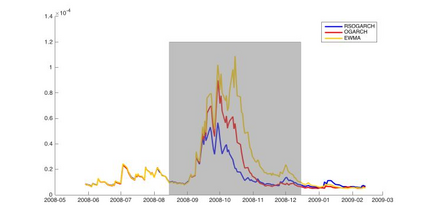
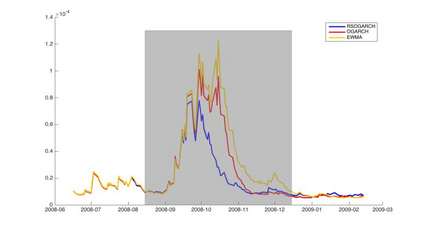
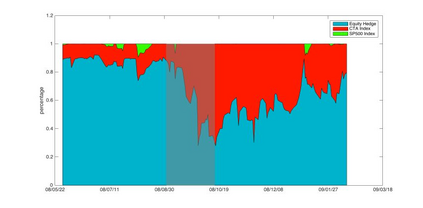
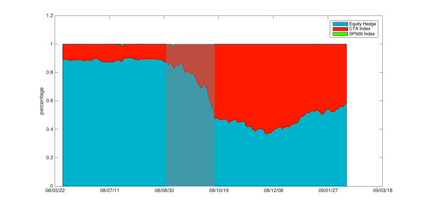
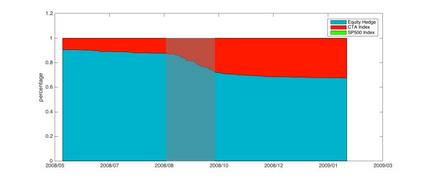
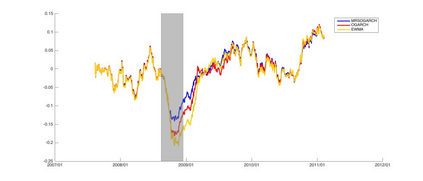
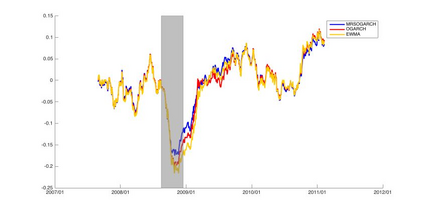
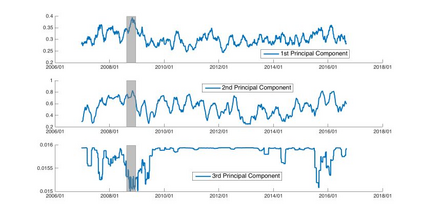
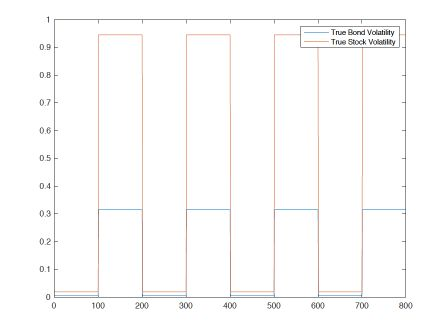
Orthogonal Generalized Autoregressive Conditional Heteroskedasticity model (OGARCH) is widely used in finance industry to produce volatility and correlation forecasts. We show that the classic OGARCH model, nevertheless, tends to be too slow in reflecting sudden changes in market condition due to excessive persistence of the integral univariate GARCH processes. To obtain more flexibility to accommodate abrupt market changes, e.g. financial crisis, we extend classic OGARCH model by incorporating a two-state Markov regime-switching GARCH process. This novel construction allows us to capture recurrent systemic regime shifts. Empirical results show that this generalization resolves the problem of excessive persistency effectively and greatly enhances OGARCH's ability to adapt to sudden market breaks while preserving OGARCH's most attractive features such as dimension reduction and multi-step ahead forecasting. By constructing a global minimum variance portfolio (GMVP), we are able to demonstrate significant outperformance of the extended model over the classic OGARCH model and the commonly used Exponentially Weighted Moving Average (EWMA) model. In addition, we show that the extended model is superior to OGARCH and EWMA in terms of predictive accuracy.
翻译:金融业广泛使用典型的OGARCH模型(OGARCH)来产生波动性和相关性预测,但我们表明,由于一体化的单向统一GARCH过程的过度持续,典型的OGARCH模型在反映市场条件突变方面往往过于缓慢,因为整体的单向统一GARCH过程的过度持续,造成市场条件的突然变化。为了获得更大的灵活性以适应突然的市场变化,例如金融危机等,我们推广了传统的OGARCH模型,纳入了两个州马克夫政权对GARCH的抽动过程。这种新颖的构造使我们能够捕捉到经常性的系统性制度变化。经验性结果表明,这种普遍化能够有效解决过度的持久性问题,大大增强OGARCH适应突然市场崩溃的能力,同时保留OGARCH最有吸引力的特征,如尺寸降低和多步预测。通过构建全球最低差异组合,我们能够展示扩展模型在典型的OGARCH模型和常用的显微动动平均模型(EWMA)预测的显著性优劣性。此外,我们还展示了AWMA模型的精确性。