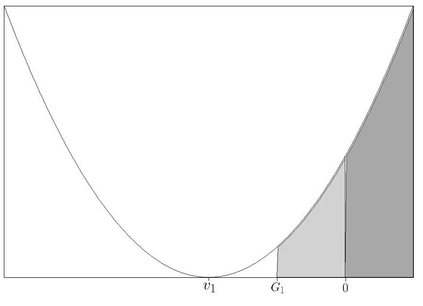
动态假设试验的理论和重大偏离:Neyman-Pearson、Min-Max和Bayesian试验 (Decision Theory and Large Deviations for Dynamical Hypotheses Test: Neyman-Pearson, Min-Max and Bayesian Tests)

We analyze hypotheses tests via classical results on large deviations for the case of two different Holder Gibbs probabilities. The main difference for the the classical hypotheses tests in Decision Theory is that here the two considered measures are singular with respect to each other. We analyze the classical Neyman-Pearson test showing its optimality. This test becomes exponentially better when compared to other alternative tests, with the sample size going to infinity. We also consider both, the Min-Max and a certain type of Bayesian hypotheses tests. We shall consider these tests in the log likelihood framework by using several tools of Thermodynamic Formalism. Versions of the Stein's Lemma and the Chernoff's information are also presented.

翻译：我们通过古典结果分析两种不同的Holder Gibbs概率的大型偏差的假设测试。在判决理论中古典假设测试的主要区别是,这里这两种考虑的测量方法相互之间是独特的。我们分析了古典Neyman-Pearson测试, 表明其最佳性。与其他替代测试相比, 样本大小将变得无限, 这一测试变得指数性更好。我们还考虑Min-Max和某种巴伊西亚假假设测试。我们将通过使用热力学形式主义的几种工具, 在日志概率框架中考虑这些测试。还提供了Stein's Lemma 和 Chernoff 的信息版本。