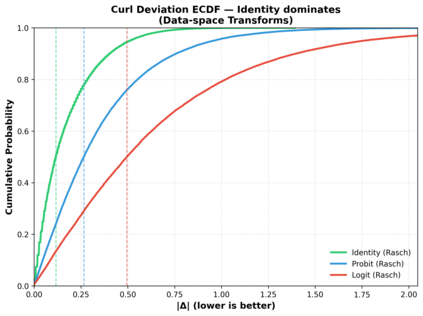
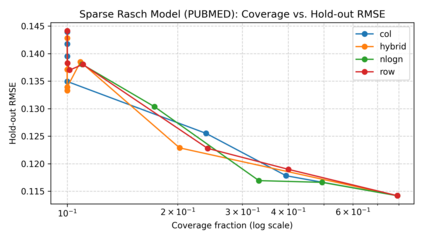
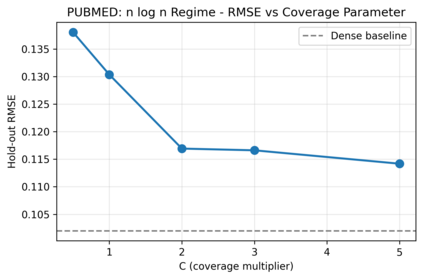
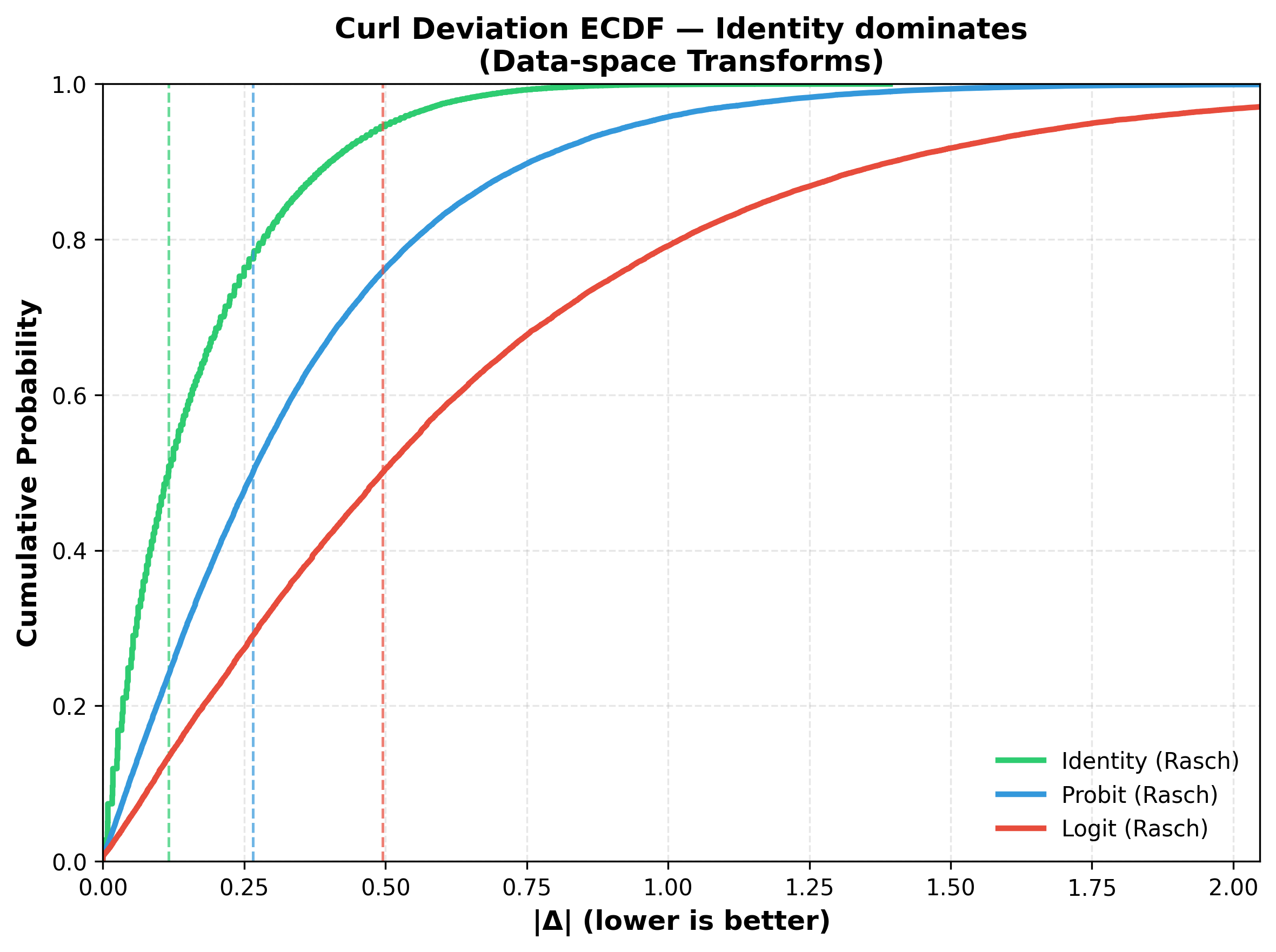
Pairwise comparisons of large language models using total variation distance mutual information (TVD-MI) produce binary critic decisions per pair. We show that averaging TVD-MI's binary trials yields centered-probability scores with additive structure suitable for item-response theory (IRT) without nonlinear link functions. Maximum-likelihood approaches to IRT use logistic links, but we find empirically that these transformations introduce curvature that breaks additivity: across three domains, the identity link yields median curl on raw data of 0.080-0.150 (P95 = [0.474, 0.580]), whereas probit/logit introduce substantially higher violations (median [0.245, 0.588], P95 [0.825, 2.252]). We derive this clipped-linear model from Gini entropy maximization, yielding a box-constrained least-squares formulation that handles boundary saturation. At 33% coverage, we achieve holdout RMSE $0.117 \pm 0.008$ while preserving agent rankings (Spearman $\rho = 0.972 \pm 0.015$), three times fewer evaluations than full dense. Judge robustness analysis (GPT-4o-mini vs. Llama3-70b) shows strong agreement in agent rankings ($\rho = 0.872$) and consistent identity-link advantage. TVD-MI's geometry is best preserved by identity mapping for efficient LLM evaluation, applicable to other bounded-response domains.
翻译:暂无翻译