word2vec, node2vec, graph2vec, X2vec：构建向量嵌入表示理论，120页ppt

Martin Grohe是一位计算机科学家，以其在参数化复杂性、数学逻辑、有限模型理论、图形逻辑、数据库理论和描述复杂性理论方面的研究而闻名。他是RWTH Aachen大学的计算机科学教授，在那里他担任离散系统逻辑和理论的主席。1999年，他获得了德国研究基金会颁发的海因茨·梅尔-莱布尼茨奖。他在2017年被选为ACM Fellow，因为他“对计算机科学中的逻辑、数据库理论、算法和计算复杂性的贡献”。

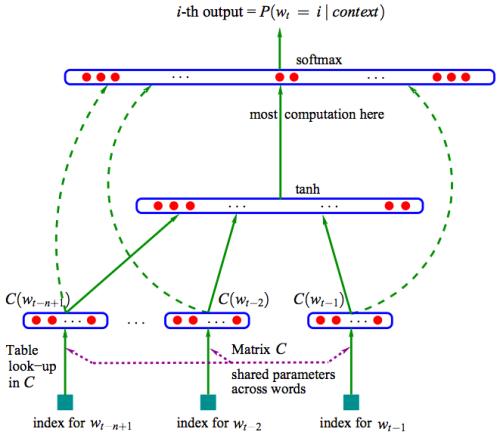
word2vec, node2vec, graph2vec, X2vec: Towards a Theory of Vector Embeddings of Structured Data 构建结构数据的向量嵌入理论

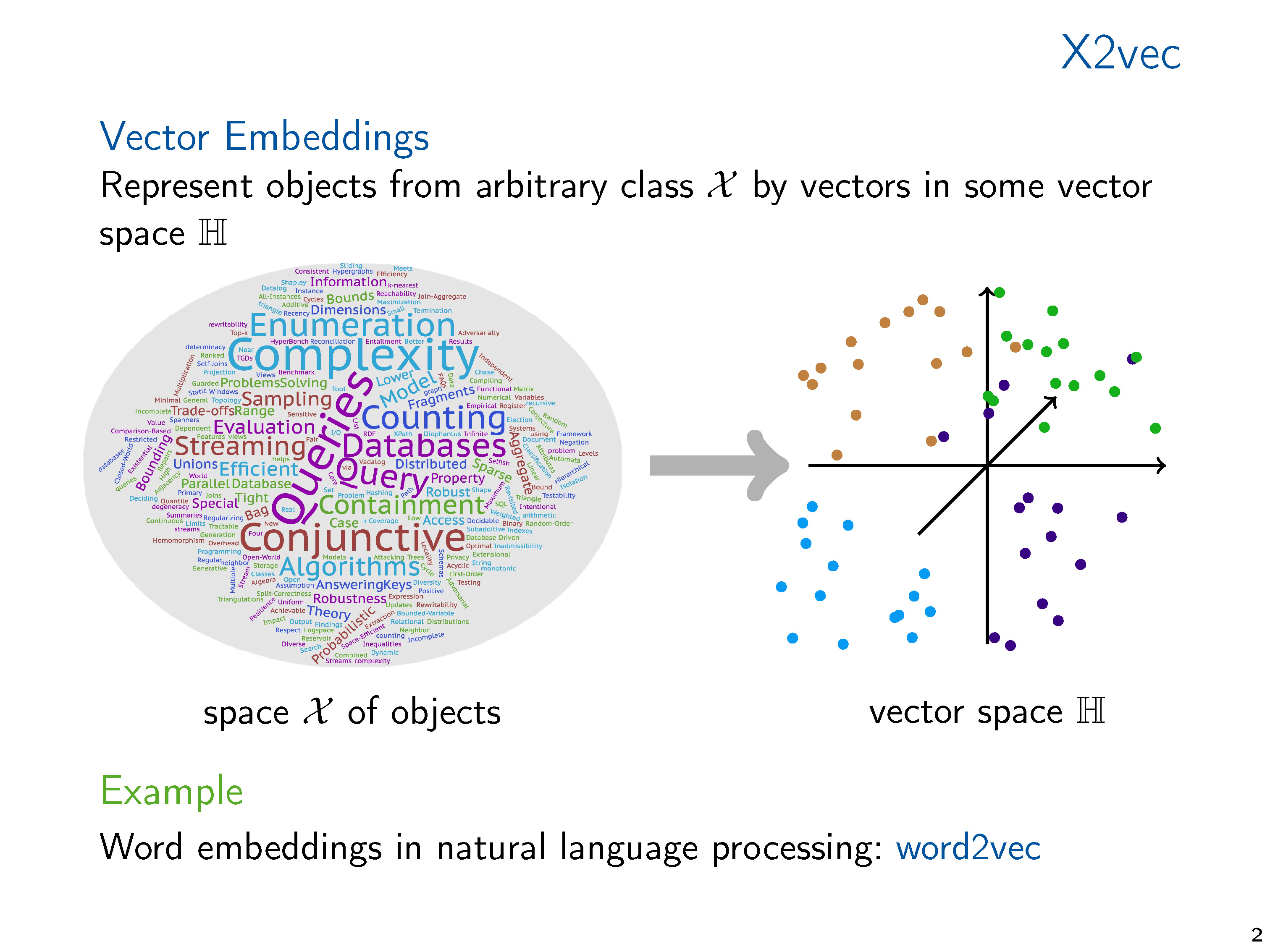
图和关系结构的向量表示，无论是手工制作的特征向量还是学习的表示，使我们能够将标准的数据分析和机器学习技术应用到结构中。在机器学习和知识表示文献中，广泛研究了产生这种嵌入的方法。然而，从理论的角度来看，向量嵌入得到的关注相对较少。从对已经在实践中使用的嵌入技术的调研开始，在这次演讲中，我们提出了两种理论方法，我们认为它们是理解向量嵌入基础的中心。我们将各种方法联系起来，并提出未来研究的方向。

典型机器学习算法需要将通常是符号数据表示为数字向量才能在结构化数据上计算。数据的向量表示从手工设计特征到学习表示，或者通过专用的嵌入算法计算，或者通过像图神经网络这样的学习架构隐式计算。机器学习方法的性能关键取决于向量表示的质量。因此，有大量的研究提出了广泛的矢量嵌入方法用于各种应用。这些研究大多是经验性的，通常针对特定的应用领域。考虑到主题的重要性，关于向量嵌入的理论工作少得令人惊讶，特别是当它表示超越度量信息(即图中的距离)的结构信息时。

本文的目的是概述在实践中使用的结构化数据的各种嵌入技术，并介绍可以理解和分析这些嵌入技术的理论思想。矢量嵌入的研究前景是笨拙的，由于不同的应用领域(如社会网络分析、知识图、化学信息学、计算生物学等)的推动，几个社区在很大程度上独立地研究相关问题。因此，我们需要有选择性，关注我们看到的共同想法和联系。

向量嵌入可以在关系数据的“离散”世界和机器学习的“可微分”世界之间架起一座桥梁，因此在数据库研究方面具有巨大的潜力。然而，除了知识图谱的二元关系之外，对关系数据的嵌入所做的工作相对较少。在整个论文中，我将试图指出关于向量嵌入的数据库相关研究问题的潜在方向。