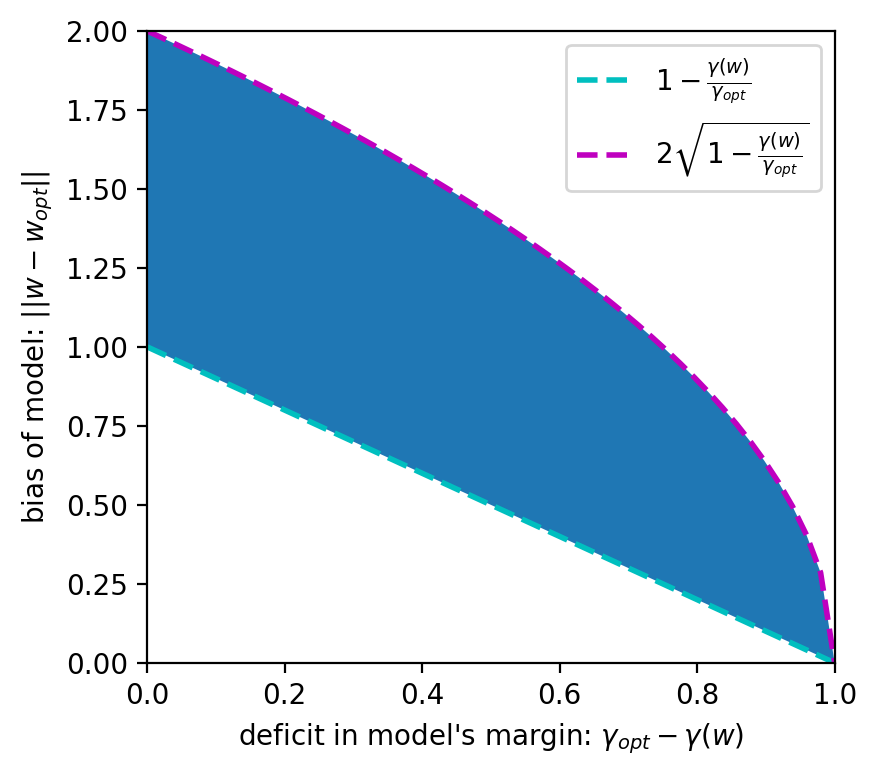
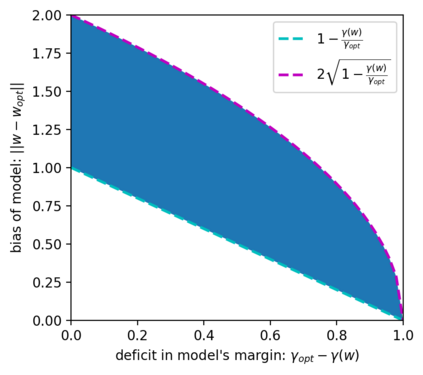
Consider $n$ points $x_1$,\ldots,$x_n$ in finite-dimensional euclidean space, each having one of two colors. Suppose there exists a separating hyperplane (identified with its unit normal vector $w)$ for the points, i.e a hyperplane such that points of same color lie on the same side of the hyperplane. We measure the quality of such a hyperplane by its margin $\gamma(w)$, defined as minimum distance between any of the points $x_i$ and the hyperplane. In this paper, we prove that the margin function $\gamma$ satisfies a nonsmooth Kurdyka-Lojasiewicz inequality with exponent $1/2$. This result has far-reaching consequences. For example, let $\gamma^{opt}$ be the maximum possible margin for the problem and let $w^{opt}$ be the parameter for the hyperplane which attains this value. Given any other separating hyperplane with parameter $w$, let $d(w):=\|w-w^{opt}\|$ be the euclidean distance between $w$ and $w^{opt}$, also called the bias of $w$. From the previous KL-inequality, we deduce that $(\gamma^{opt}-\gamma(w)) / R \le d(w) \le 2\sqrt{(\gamma^{opt}-\gamma(w))/\gamma^{opt}}$, where $R:=\max_i \|x_i\|$ is the maximum distance of the points $x_i$ from the origin. Consequently, for any optimization algorithm (gradient-descent or not), the bias of the iterates converges at least as fast as the square-root of the rate of their convergence of the margin. Thus, our work provides a generic tool for analyzing the implicit bias of any algorithm in terms of its margin, in situations where a specialized analysis might not be available: it is sufficient to establish a good rate for converge of the margin, a task which is usually much easier.
翻译:考虑 $x_ 1 美元,\ lidots, $x_ n美元, 在有限维度的 euclide 空间中, 每个都有两种颜色之一 。 如果在点上存在一个相隔的超平面( 单位正向矢量 $w) 美元, 也就是高平面的点, 其最大颜色点位于高平面的同一侧面上。 我们用它的差值 $\ gamma (w) 来测量这种超平面的质量 $( x_ i) 和超平面空间的最小距离 。 在本文中, 我们证明 $\ gamma 通常满足的是非摩特的 库尔迪卡- Lojasiewicz 不平等 $ww) 。 这个结果具有深远的影响。 例如, $\ gammamap 美元 是问题的最大可能的差值, 并且让 $@ opt$( lax) 作为超平面值的值的参数 。