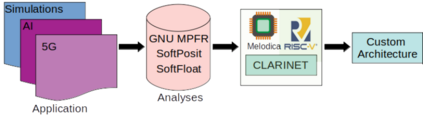
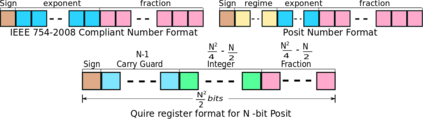
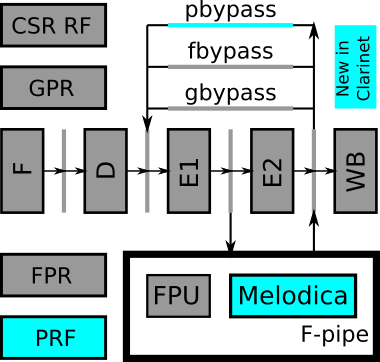
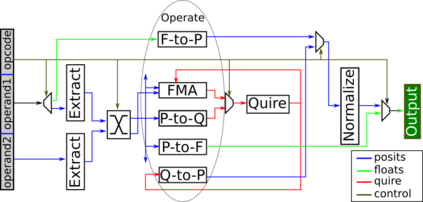
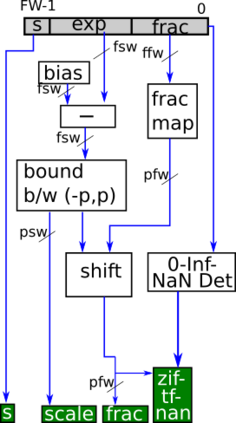
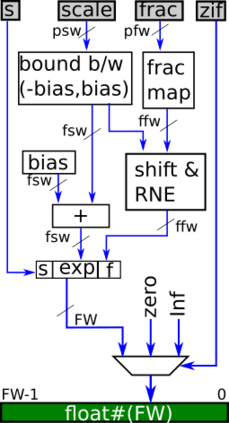
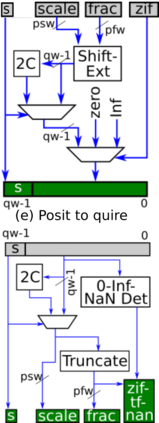
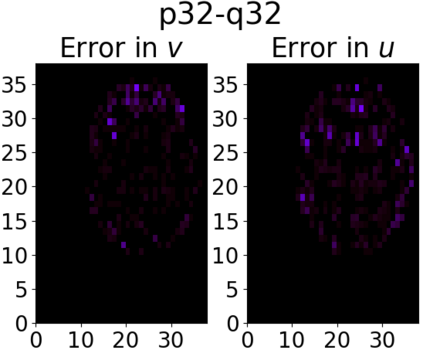
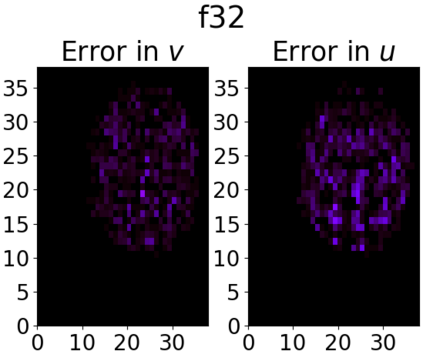
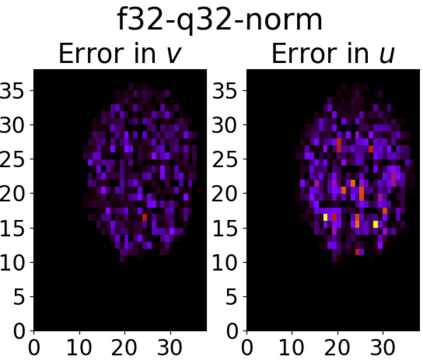
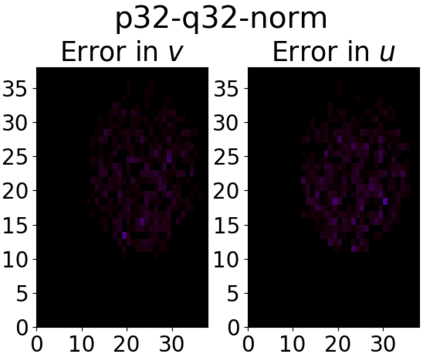
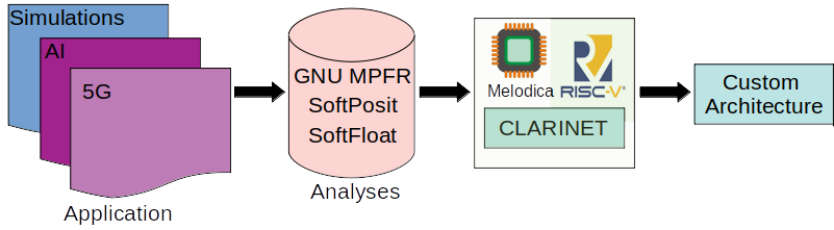
Many engineering and scientific applications require high precision arithmetic. IEEE 754-2008 compliant (floating-point) arithmetic is the de facto standard for performing these computations. Recently, posit arithmetic has been proposed as a drop-in replacement for floating-point arithmetic. The posit data representation and arithmetic offer several absolute advantages over the floating-point format and arithmetic including higher dynamic range, better accuracy, and superior performance-area trade-offs. In this paper, we present a consolidated general-purpose processor-based framework to support posit arithmetic empiricism. The end-users of the framework have the liberty to seamlessly experiment with their applications using posit and floating-point arithmetic since the framework is designed for the two number systems to coexist. The framework consists of Melodica and Clarinet. Melodica is a posit arithmetic core that implements parametric fused-multiply-accumulate and, more importantly, supports the quire data type. Clarinet is a Melodica-enabled processor based on the RISC-V ISA. To the best of our knowledge, this is the first-ever integration of quire to a RISC-V core. To show the effectiveness of the Clarinet platform, we perform an extensive application study and benchmarking on some of the common linear algebra and computer vision kernels. We perform ASIC synthesis of Clarinet and Melodica on a 90 nm-CMOS Faraday process. Finally, based on our analysis and synthesis results, we define a quality metric for the different instances of Clarinet that gives us initial recommendations on the goodness of the instances. Clarinet-Melodica is an easy-to-experiment platform that will be made available in open-source for posit arithmetic empiricism.
翻译:许多工程和科学应用都需要高精密的算术。 IEEE 754-2008符合(浮点点)的算术是进行这些计算的实际标准。 最近,提出了假设算术,作为浮动点算术的递进替代。 假设数据表示和算术为浮点格式和算术提供了若干绝对的优势, 包括更高的动态范围、 更好的准确度和高级性能- 地区取舍。 在本文中, 我们提出了一个基于通用处理器的综合框架, 以支持算术判断。 框架的最终用户可以自由地使用正点和浮点算术进行其应用的无缝实验。 由于框架是为两个数字系统设计要共存而设计的, 假设算术的算术是一个绝对的计算核心, 包括更高的动态范围、 更好的精确度、 高级性能和高级性能。 克拉里( Clarinet) 是一个基于RISC- V ISA 的美洛迪程序, 。 我们最了解的是,这是首次将正基的正基数质量整合到一个我们IMISC 初步的直径直径直径分析过程核心。