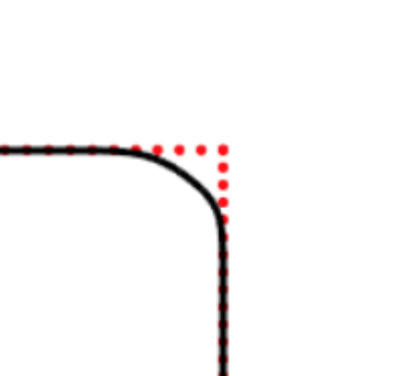
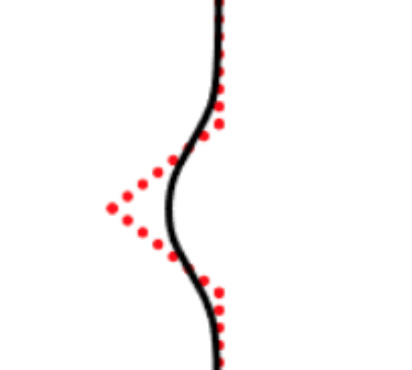
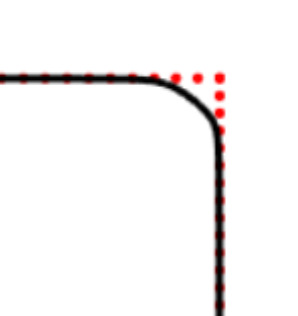
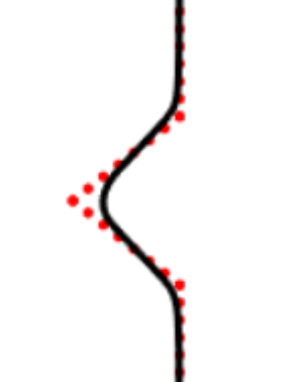
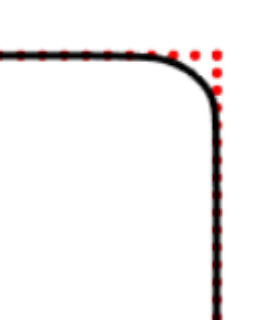
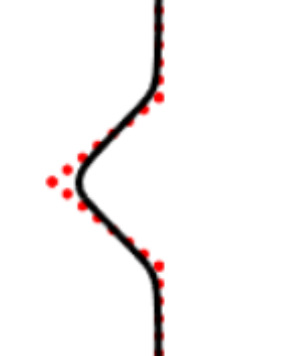
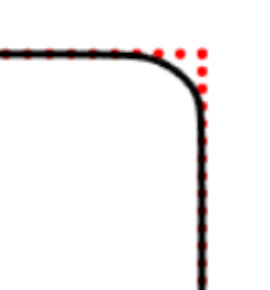
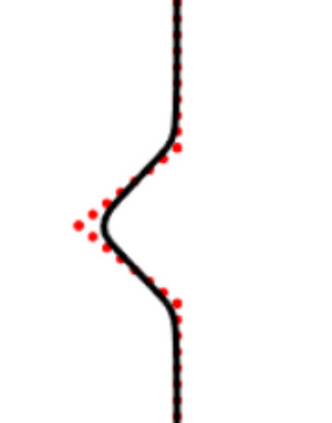
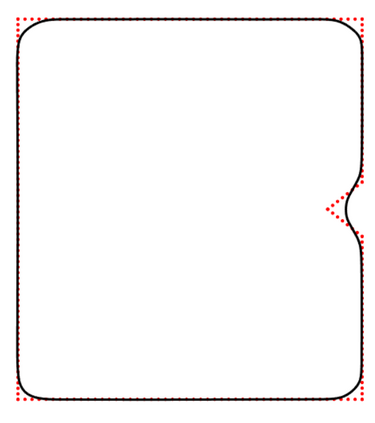
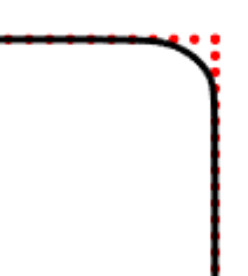
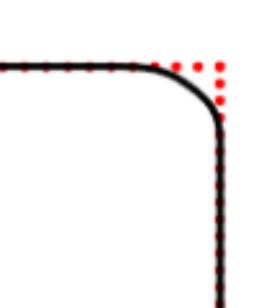
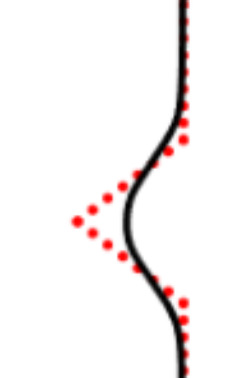
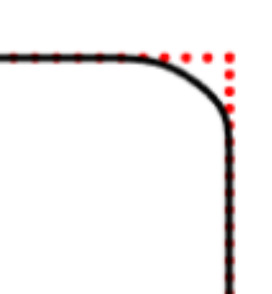
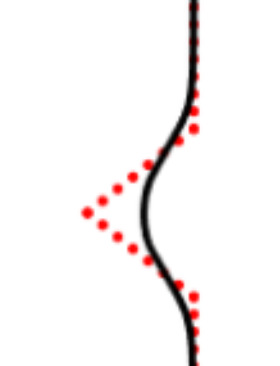
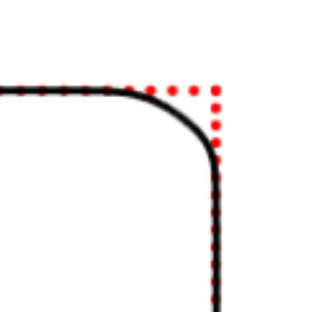
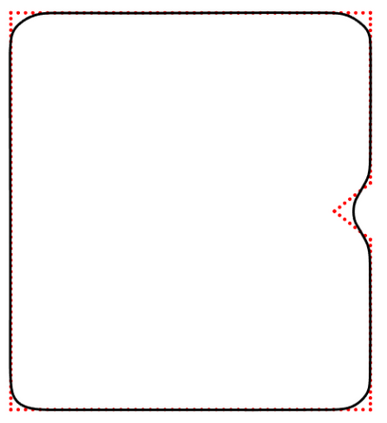
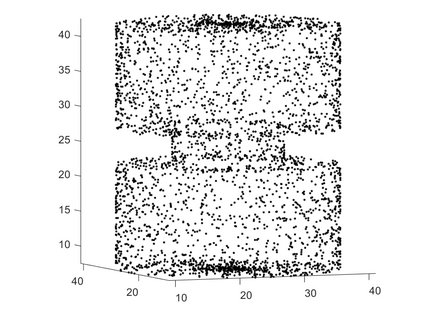
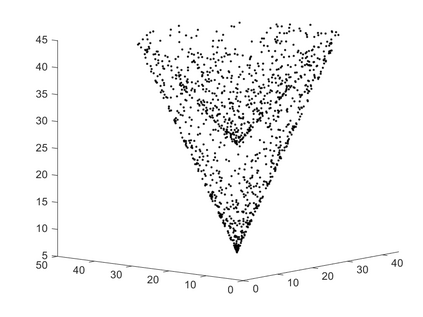
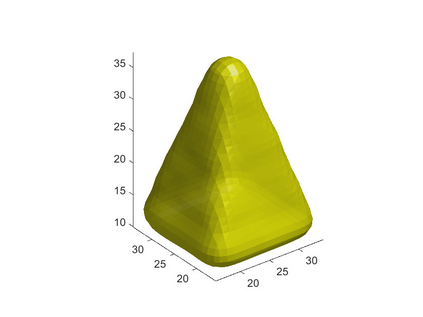
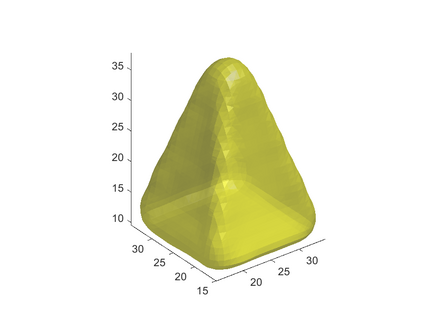
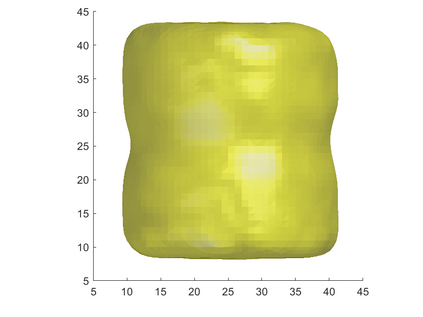
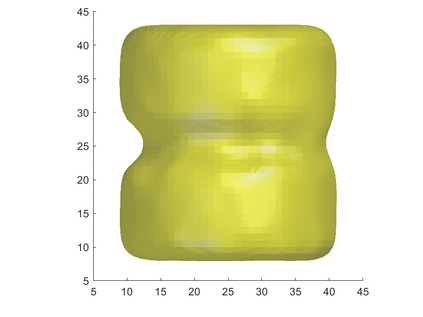
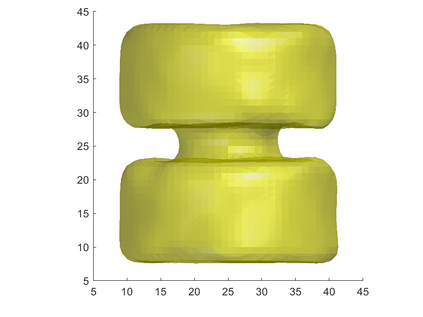
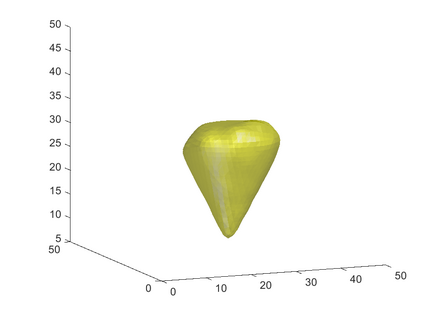
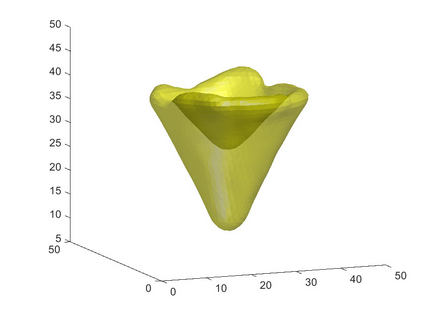
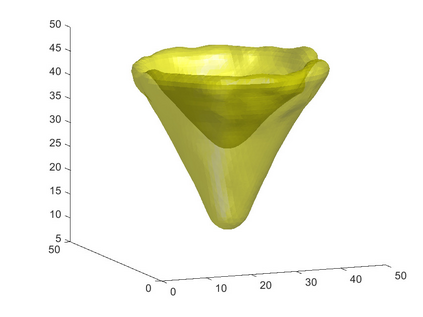
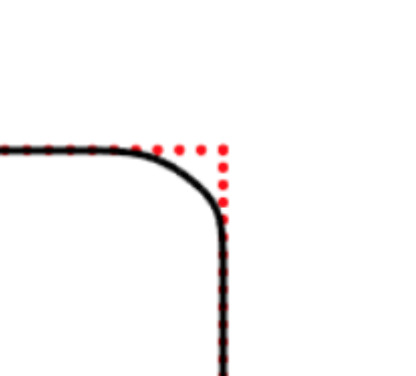
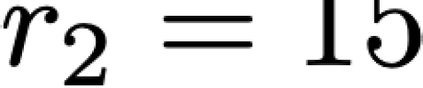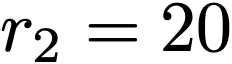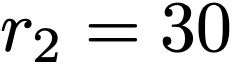We propose a variational functional and fast algorithms to reconstruct implicit surface from point cloud data with a curvature constraint. The minimizing functional balances the distance function from the point cloud and the mean curvature term. Only the point location is used, without any local normal or curvature estimation at each point. With the added curvature constraint, the computation becomes particularly challenging. To enhance the computational efficiency, we solve the problem by a novel operator splitting scheme. It replaces the original high-order PDEs by a decoupled PDE system, which is solved by a semi-implicit method. We also discuss approach using an augmented Lagrangian method. The proposed method shows robustness against noise, and recovers concave features and sharp corners better compared to models without curvature constraint. Numerical experiments in two and three dimensional data sets, noisy and sparse data are presented to validate the model.
翻译:我们提出一个变式功能和快速算法,用曲线限制从点云数据重建隐含表面。 最小化功能平衡点云和平均曲线术语的距离功能。 仅使用点位置, 没有在每一点进行任何本地的正常或曲线估计。 由于附加的曲线限制, 计算变得特别具有挑战性。 为了提高计算效率, 我们通过一个新的操作员分割方案来解决问题。 它用一个分解的 PDE 系统来取代原高阶 PDE 系统, 该系统通过半隐形方法解决。 我们还讨论使用增强的 Lagrangian 方法的方法的方法。 拟议的方法显示对噪音的稳健性, 并恢复组合特征和尖锐角, 与模型相比, 没有曲线限制。 在两个和三个维数据集中进行数字性实验, 以杂乱和分散的数据来验证模型。