这本417页的数学基础，还没出版就能免费下载啦！

来自： 程序员书库（ID： CodingBook）

Marc Peter Deisenroth，A Aldo Faisal 和 Cheng Soon Ong 撰写了一本《机器学习数学基础》，目前已经可以免费下载，该书将于2020年初由剑桥大学出版社出版。

根据官网介绍，本书将于2020年由剑桥大学出版社出版。

如果你看到书名《机器学习数学基础》就想退出去，那你真是想错了，本书并不打算过多的讲授先进的机器学习技术，因为类似的书籍已经有很多了，作者更多的是把重心放在数学知识上，这样一来，你再去阅读其他机器学习相关的书籍就会轻松很多

我也是在网站查找机器学习相关的数学资料时发现了这本书，虽然我没有在这本书身上花太多时间，但是里面的原理已经足够我的ML研究，而且每章都有一些练习或者编程教程，这是非常不错的。

本书的章节分布如下：

第一部分：数学基础

• Introduction and Motivation

• Linear Algebra

• Analytic Geometry

• Matrix Decompositions

• Vector Calculus

• Probability and Distribution

• Continuous Optimization

第二部分：机器学习问题

• When Models Meet Data

• Linear Regression

• Dimensionality Reduction with Principal Component Analysis

• Density Estimation with Gaussian Mixture Models

• Classification with Support Vector Machines

接下来，我们一起来看看作者在第一部分的数学基础，都和我们介绍了哪些内容？

第一章（介绍和目的） ，顾名思义就是介绍这本书，并定义一些将要涉及到的单词和概念，如预测器、培训、模型等。它还推荐了两种阅读方法，自底向上方法(“从基础到更高级的概念构建”)和自顶向下策略(“从实际需求到更底层的知识进行阅读”)。我采用了自下而上的策略，最后，本章以大约两页的篇幅简要描述了本书的所有章节。

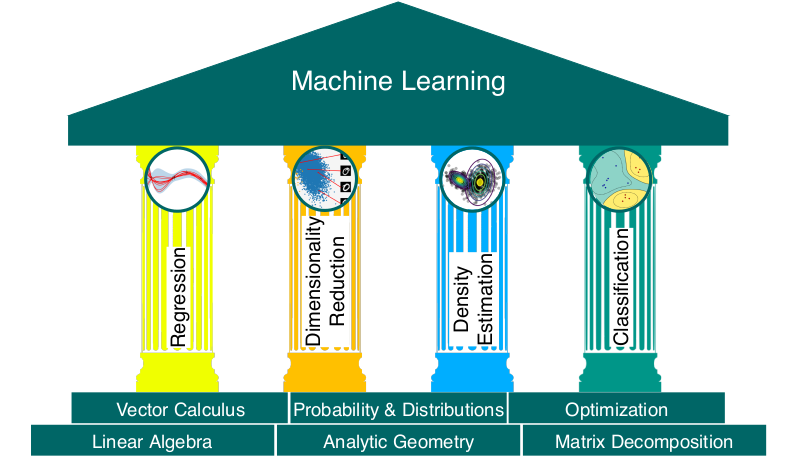
第2章、第3章和第4章描述了线性代数的整个领域，作者分别把他们拆分成三个小部分： 线性代数、解析几何、矩阵分解，这样做的目的，我猜是为了让每一章都可以简单而又模块化，而不是一个整体而又庞大章节。

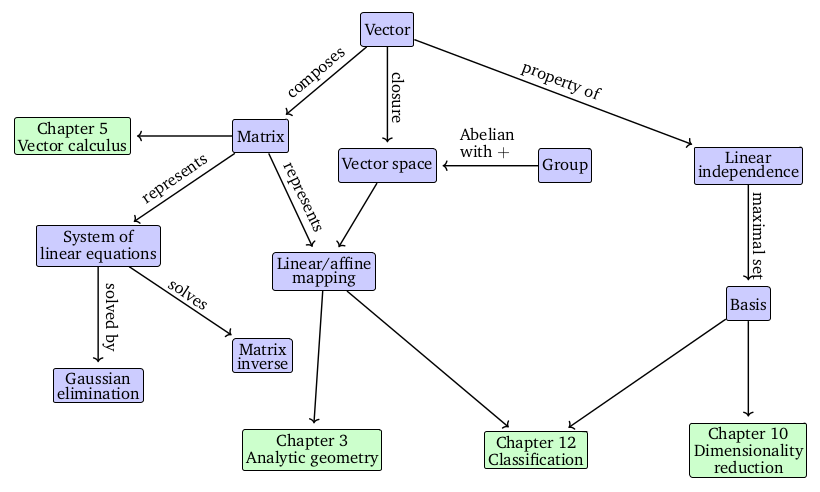
第2章的“线性代数” ，从最基本的高中数学概念开始介绍（系统的线性方程、矩阵、高斯消除法、摩尔彭罗斯伪逆）到更抽象的概念，如向量空间和之空间，线性无关，同态、仿射等。

第二章的思维导图：

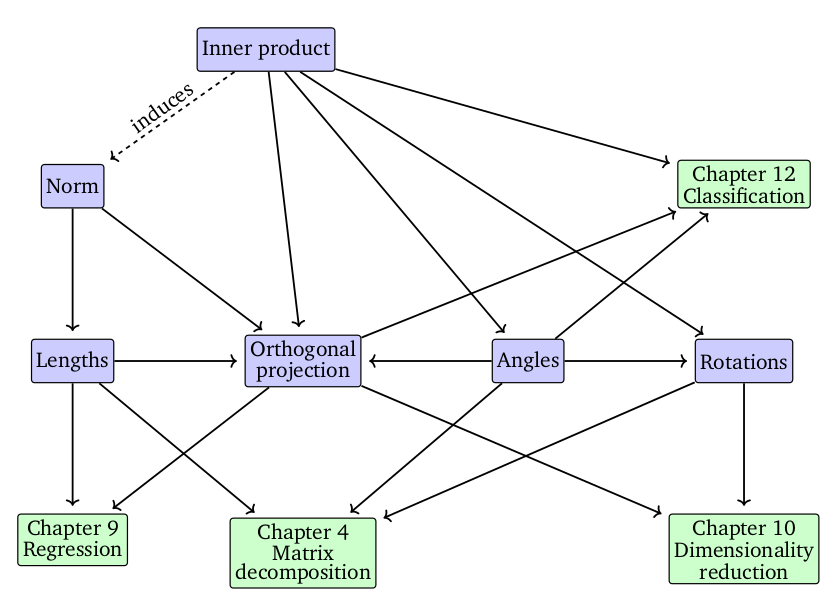
在第三章(“解析几何”)中 ，该书使用了前一章的抽象概念来定义几何元素：向量内积、角度和正交性、投影和旋转等，值得一提的是，书中所有的操作都是先用2D/3D来描述，然后深入到n-D，第三章的思维导图如下：

最后一章题为“矩阵分解” ，它是非常有趣的并且十分重要，相对前面两章，这一章多了一些现实应用的例子，如Google的pagerank实现。

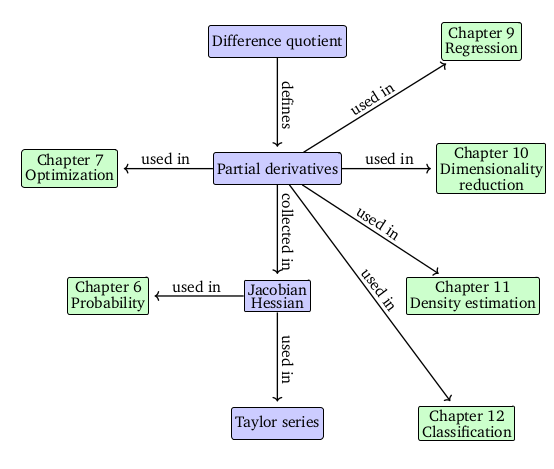
第5章是关于向量微积分 的，在我听来非常侧重于ML的基本优化理论，它描述了(偏微分)、泰勒级数、链式法则、梯度、矩阵微积分、反向传播和自动微分，以及一些高阶导数和线性化。

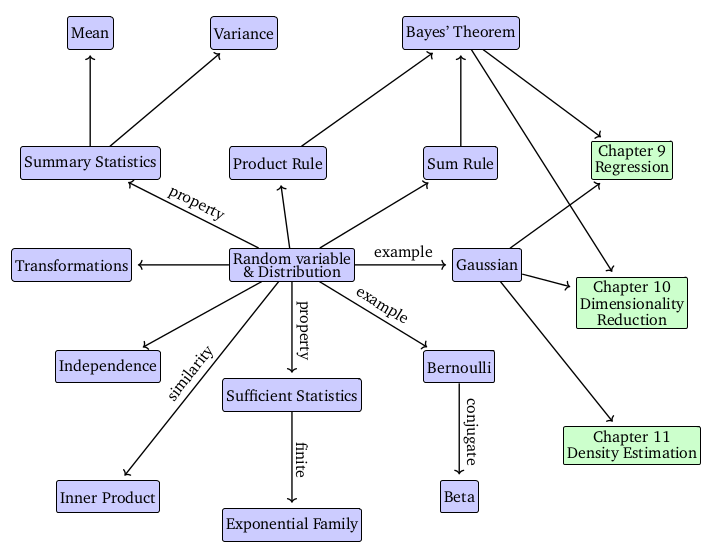
第六章是“概率与分布” 。主要内容包括基本概率与统计、随机变量、离散与连续分布、贝叶斯定理、概论统计、统计独立性、高斯分布、共轭性质、变量替换等。

数学基础部分的最后一章是连续优化，我把这一章当成ML基础的开始，尽管它在大学的课程里并不总涉及到，就算有也只是表面，本章介绍了梯度下降、动量、约束优化(使用拉格朗日乘子)、凸优化、线性等。

最后附上本书相关的地址，你也可以通过后台回复【shuku】的方式获得本书

下载链接：https://mml-book.github.io/book/mml-book.pdf

书籍官网： http s://mml-book.github.io/

---

●编号4073，输入编号直达本文

●输入m获取文章目录

推荐↓↓↓

程序员数学之美

更多推荐《25个技术类公众微信》

涵盖：程序人生、算法与数据结构、黑客技术与网络安全、大数据技术、前端开发、Java、Python、Web开发、安卓开发、iOS开发、C/C++、.NET、Linux、数据库、运维等。