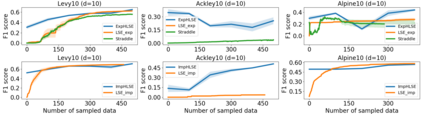
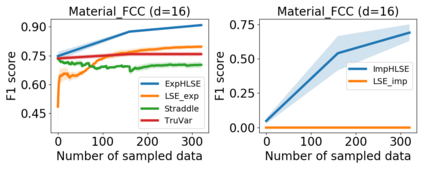
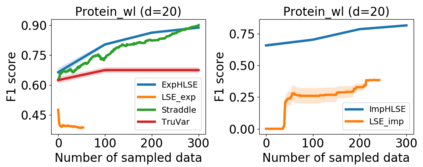
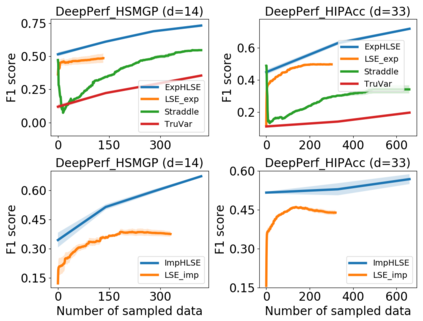
Level Set Estimation (LSE) is an important problem with applications in various fields such as material design, biotechnology, machine operational testing, etc. Existing techniques suffer from the scalability issue, that is, these methods do not work well with high dimensional inputs. This paper proposes novel methods to solve the high dimensional LSE problems using Bayesian Neural Networks. In particular, we consider two types of LSE problems: (1) \textit{explicit} LSE problem where the threshold level is a fixed user-specified value, and, (2) \textit{implicit} LSE problem where the threshold level is defined as a percentage of the (unknown) maximum of the objective function. For each problem, we derive the corresponding theoretic information based acquisition function to sample the data points so as to maximally increase the level set accuracy. Furthermore, we also analyse the theoretical time complexity of our proposed acquisition functions, and suggest a practical methodology to efficiently tune the network hyper-parameters to achieve high model accuracy. Numerical experiments on both synthetic and real-world datasets show that our proposed method can achieve better results compared to existing state-of-the-art approaches.
翻译:水平定点估计(LSE)是各种应用领域应用的一个重要问题,如材料设计、生物技术、机器操作测试等。 现有技术存在可缩放性问题,即这些方法在高维投入方面效果不佳。 本文建议采用新方法解决高维LSE问题, 特别是, 我们考虑两种LSE问题:(1)\textit{explit}LSE问题, 阈值是固定用户指定值, (2)\textit{imcit}LSE问题, 将阈值定义为目标功能( 未知) 最大百分比的百分比。 对于每一个问题, 我们得出相应的基于获取数据点的理论信息功能, 以最大限度地提高设定值的准确性。 此外, 我们还分析我们拟议获取功能的理论时间复杂性, 并提出一种实用的方法, 高效调整网络超参数, 以达到高模型精确度。 合成和真实世界数据集的数值实验显示, 我们所提议的方法可以比现有状态方法取得更好的结果。