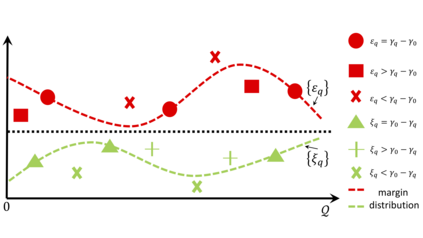
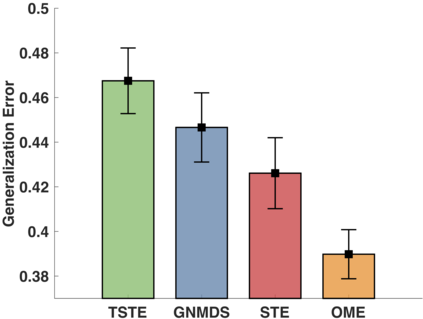
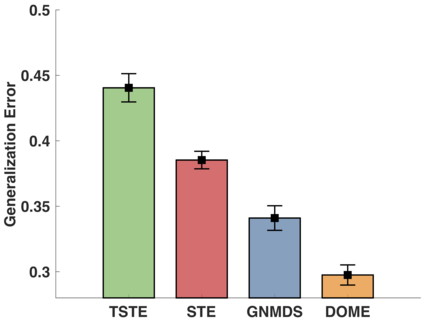
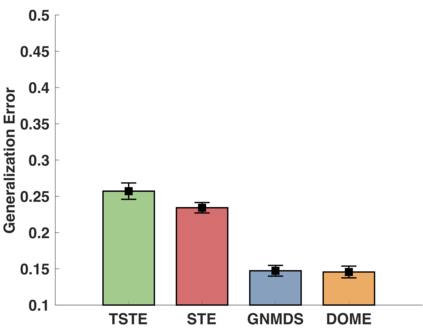
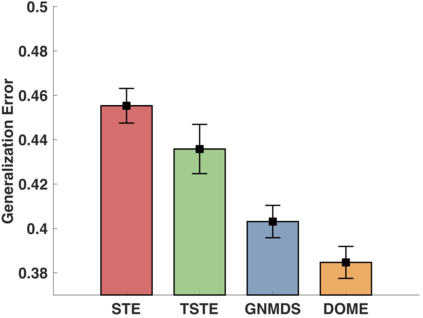
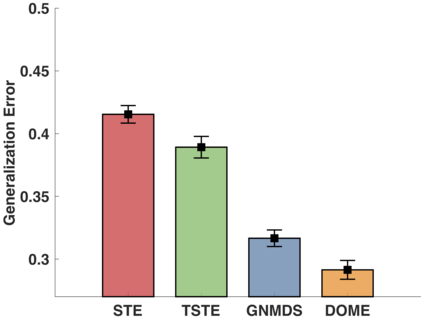
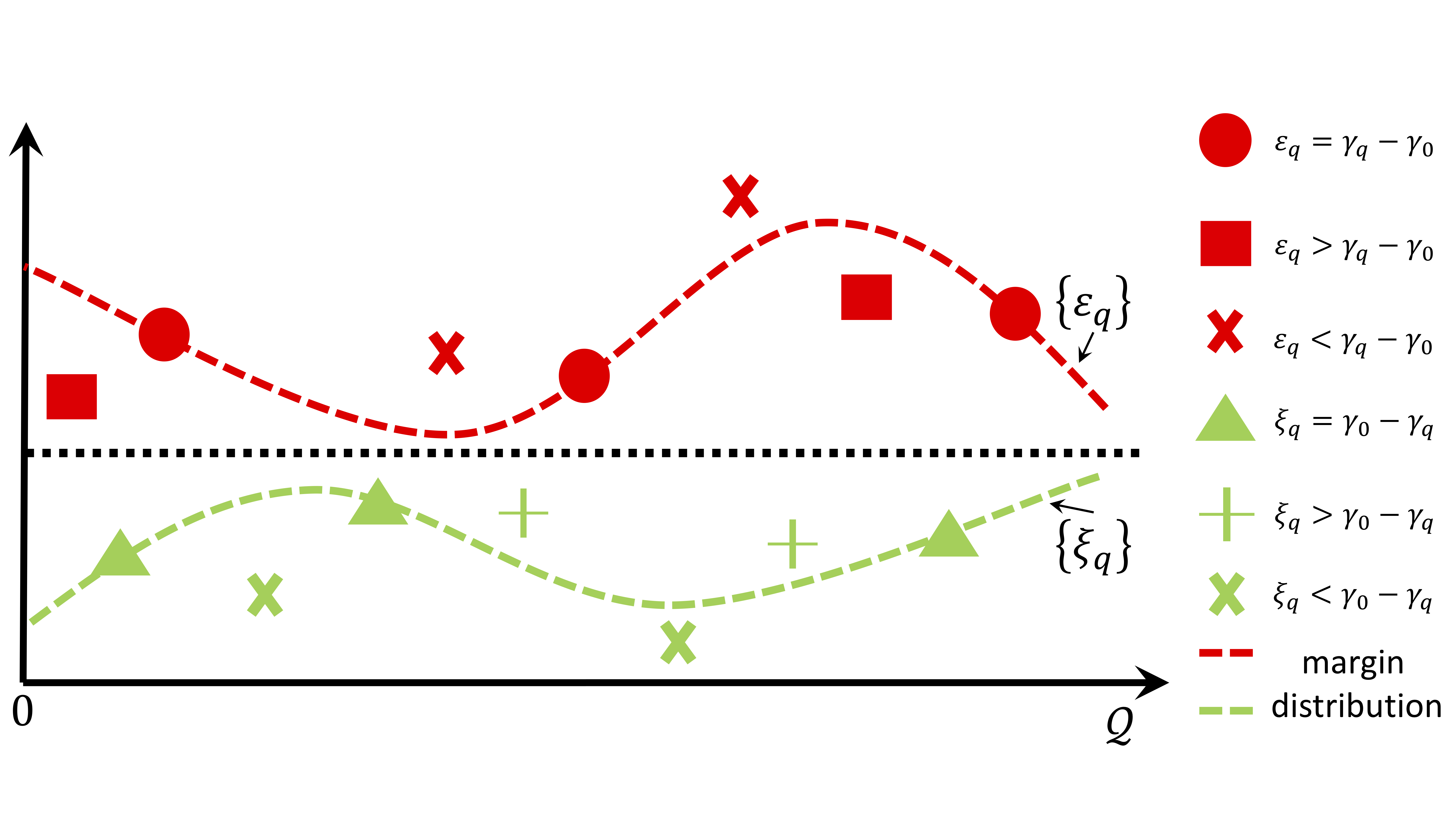
In the absence of prior knowledge, ordinal embedding methods obtain new representation for items in a low-dimensional Euclidean space via a set of quadruple-wise comparisons. These ordinal comparisons often come from human annotators, and sufficient comparisons induce the success of classical approaches. However, collecting a large number of labeled data is known as a hard task, and most of the existing work pay little attention to the generalization ability with insufficient samples. Meanwhile, recent progress in large margin theory discloses that rather than just maximizing the minimum margin, both the margin mean and variance, which characterize the margin distribution, are more crucial to the overall generalization performance. To address the issue of insufficient training samples, we propose a margin distribution learning paradigm for ordinal embedding, entitled Distributional Margin based Ordinal Embedding (\textit{DMOE}). Precisely, we first define the margin for ordinal embedding problem. Secondly, we formulate a concise objective function which avoids maximizing margin mean and minimizing margin variance directly but exhibits the similar effect. Moreover, an Augmented Lagrange Multiplier based algorithm is customized to seek the optimal solution of \textit{DMOE} effectively. Experimental studies on both simulated and real-world datasets are provided to show the effectiveness of the proposed algorithm.
翻译:在缺乏先前知识的情况下,星系嵌入方法通过一系列四倍的比较,为低维欧几里德空间的物品获得了新的代表。这些星系比较往往来自人类的注解者,而足够的比较则导致古典方法的成功。然而,收集大量标签数据被称为一项艰巨任务,而大多数现有工作很少注意样本不足的概括能力。与此同时,大差值理论最近的进展表明,不仅只是最大限度地扩大最小差值,差值分布的差值和差值,对于总体总体概括性业绩更为关键。为了解决培训样本不足的问题,我们提议为星系嵌入提供一个差值分配学习模式,题为“基于分布的边际嵌入” (\ textit{DMOE})。准确地说,我们首先界定了星系嵌问题的范围。第二,我们制定了一个简明的客观功能,避免最大差值意味着和最小差值差异,但展示了类似的效果。此外,一个基于星系多维值的多比值多比值多里尔算法系的模型研究模式是定制的,以模拟方式展示了以最佳解决方案。