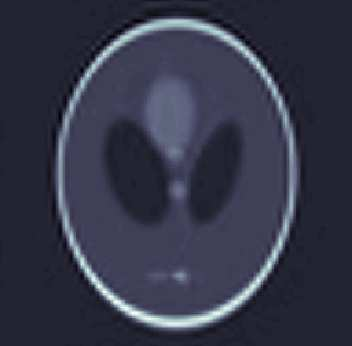
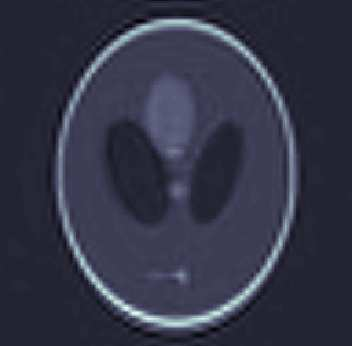
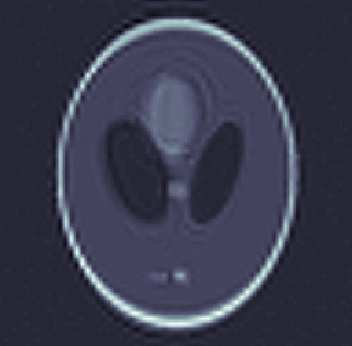
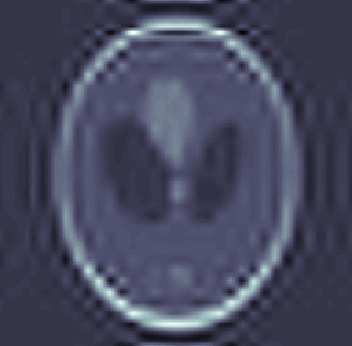
In this paper, we introduce a computational framework for recovering a high-resolution approximation of an unknown function from its low-resolution indirect measurements as well as high-resolution training observations by merging the frameworks of generalized sampling and functional principal component analysis. In particular, we increase the signal resolution via a data driven approach, which models the function of interest as a realization of a random field and leverages a training set of observations generated via the same underlying random process. We study the performance of the resulting estimation procedure and show that high-resolution recovery is indeed possible provided appropriate low-rank and angle conditions hold and provided the training set is sufficiently large relative to the desired resolution. Moreover, we show that the size of the training set can be reduced by leveraging sparse representations of the functional principal components. Furthermore, the effectiveness of the proposed reconstruction procedure is illustrated by various numerical examples.
翻译:在本文中,我们采用一个计算框架,通过将一般抽样和功能性主要组成部分分析框架合并,从低分辨率间接测量和高分辨率培训观测中回收一个未知功能的高分辨率近似值,特别是通过数据驱动方法增加信号分辨率,该方法将感兴趣的功能作为随机字段的实现模型,并利用通过同一随机过程产生的一套培训观测结果。我们研究由此得出的估计程序的绩效,并表明,如果保持适当的低级别和角度条件,而且如果培训组与预期的解决方案相比足够大,高分辨率回收的确有可能。此外,我们表明,通过利用功能性主要组成部分很少的体现,可以减少培训组的规模。此外,各种数字实例说明了拟议重建程序的有效性。