Second-Order Guarantees in Centralized, Federated and Decentralized Nonconvex Optimization

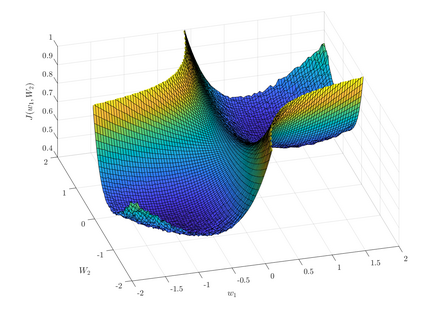
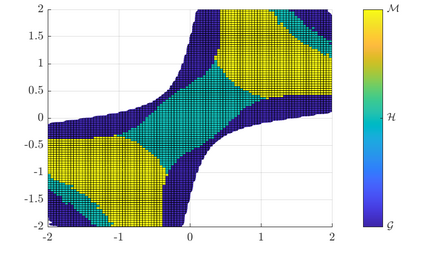
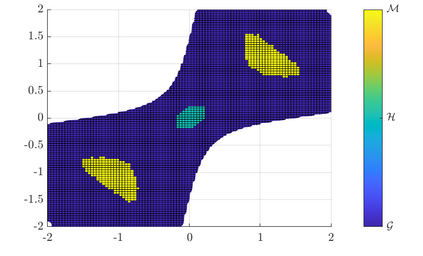
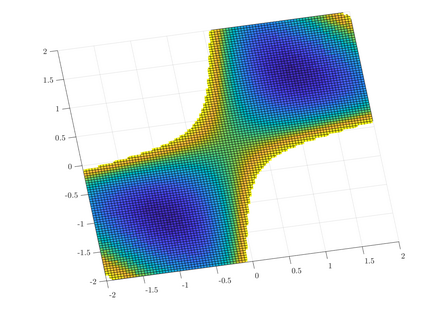
Rapid advances in data collection and processing capabilities have allowed for the use of increasingly complex models that give rise to nonconvex optimization problems. These formulations, however, can be arbitrarily difficult to solve in general, in the sense that even simply verifying that a given point is a local minimum can be NP-hard [1]. Still, some relatively simple algorithms have been shown to lead to surprisingly good empirical results in many contexts of interest. Perhaps the most prominent example is the success of the backpropagation algorithm for training neural networks. Several recent works have pursued rigorous analytical justification for this phenomenon by studying the structure of the nonconvex optimization problems and establishing that simple algorithms, such as gradient descent and its variations, perform well in converging towards local minima and avoiding saddle-points. A key insight in these analyses is that gradient perturbations play a critical role in allowing local descent algorithms to efficiently distinguish desirable from undesirable stationary points and escape from the latter. In this article, we cover recent results on second-order guarantees for stochastic first-order optimization algorithms in centralized, federated, and decentralized architectures.