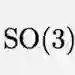【硬核书】群论，Group Theory，135页pdf

这些笔记的第一个版本是为第一年的研究生代数课程编写的。和大多数这类课程一样，讲义集中在抽象群，特别是有限群。然而，大多数数学家遇到的群并不是抽象的群，而是代数群、拓扑群或李群，而且感兴趣的不仅仅是群本身，还有它们的线性表示。我的意图是(将来的某一天)扩展笔记以考虑到这一点，并制作一本规模适中(c200页)的书，为数学、物理和相关领域的刚开始学习的研究生提供更全面的关于群论的介绍。